a la Mode - UNC Comp 101

In this problem set you will write a few functions to process arrays using algorithms. You will ultimately write an algorithm to compute the mode, or the number which occurs most often, in an array of integer numbers.

Getting Started

To begin, you should pull the latest materials using npm run pull and start your development server with npm start.

You will see a folder for ps06-a-la-mode appear. Open the index-app.ts file and complete the honor code section with your name and ONYEN.

Understanding the Skeleton Code

Spend a minute to read through the main function and the four other functions in the program (min, maxIndex, max, and mode). Notice that in the main function an array of numbers is established named input. This is just some arbitrary made-up data to help you get started with the project. As you work on implementing each function below, you should change this input data to test the correctness of your functions!

1) min

Implement the function named min to satisfy the following requirements.

When min is called with an empty array for parameter a, it should return 0.

When min is called with a non-empty array for parameter a, it should return the smallest element in the array.

For example, the following array has a minimum value of 0. This element, 0, is at index 3:

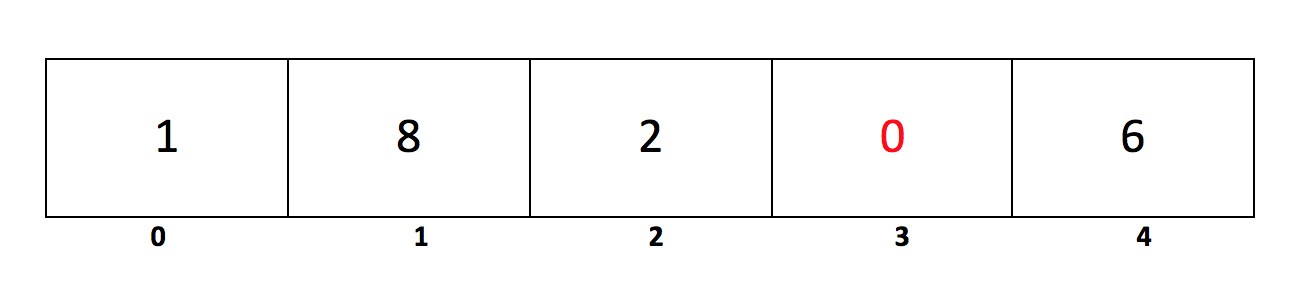
Let's think about this more in-depth. Take the following array and some arbitrary number variable currMin:

Why can we only see the element at index 0? It can be helpful to think about this array "one element at a time" when discussing looping. We can also think about some variable, currMin, that holds the value of our minimum as we know it at that moment. Right now, that is 9. Let's take a peek at our next index.

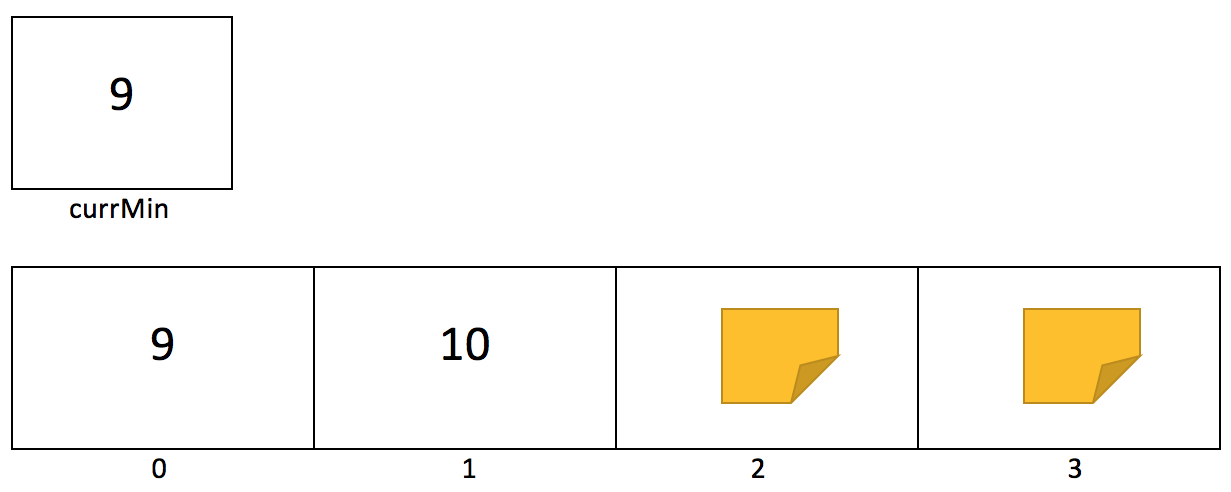
We see that index 1 holds the number 10. We compare 10 with 9 and, since 10 < 9 evaluates to false, we can continue onto the next index without changing currMin. Let's move on to see what's at index 2.

Index 2's element is 3, which is less than our currMin. Therefore, we change currMin because we know that our minimum value up to this point is now 3, not 9. Finally, let's see our last element.

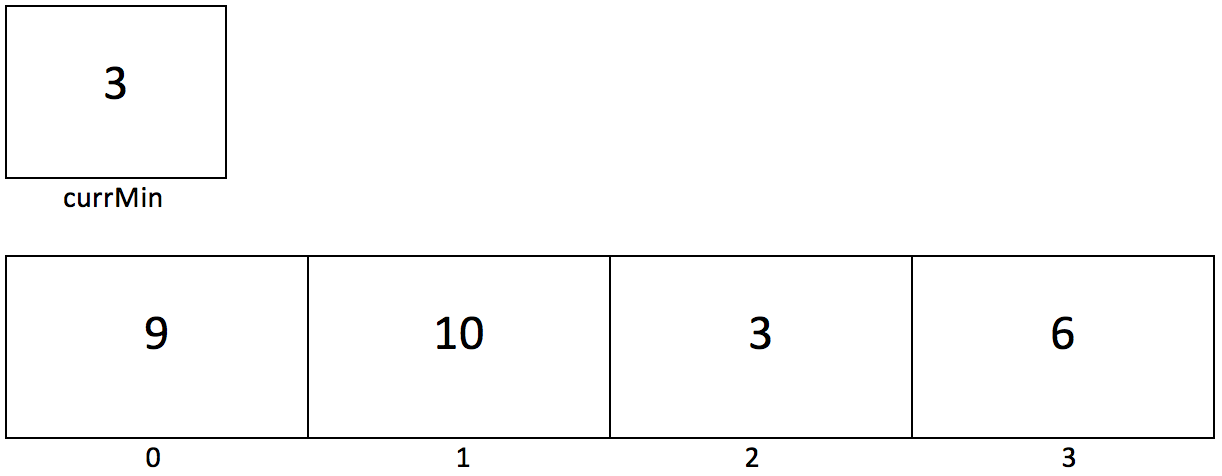
Our last element, 6, is not less than our current understanding of the minimum value. Therefore, after walking through our entire array, we know that the minimum value is 3, which we return.

2) maxIndex

Implement the function named maxIndex to satisfy the following requirements.

When maxIndex is called with an empty array for parameter a, it should return -1.

When maxIndex is called with a non-empty array for parameter a, it should return the index of the element with the largest value in the array. When there are multiple elements that are each equal to the maximum value, then return the smallest index containing the maximum value. For example, maxIndex([3, 3, 2, 1]) should return 0.

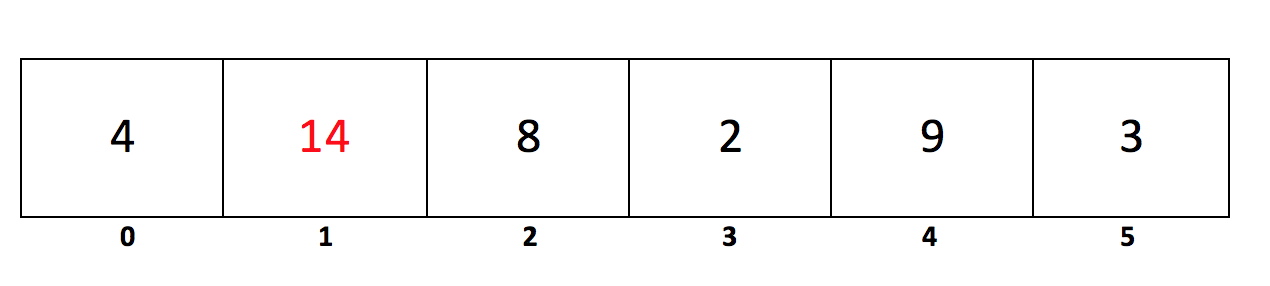
Another example would be the following array. The largest element in the array is 14, which sits at index 1. Therefore, calling maxIndex with the following array would return 1.

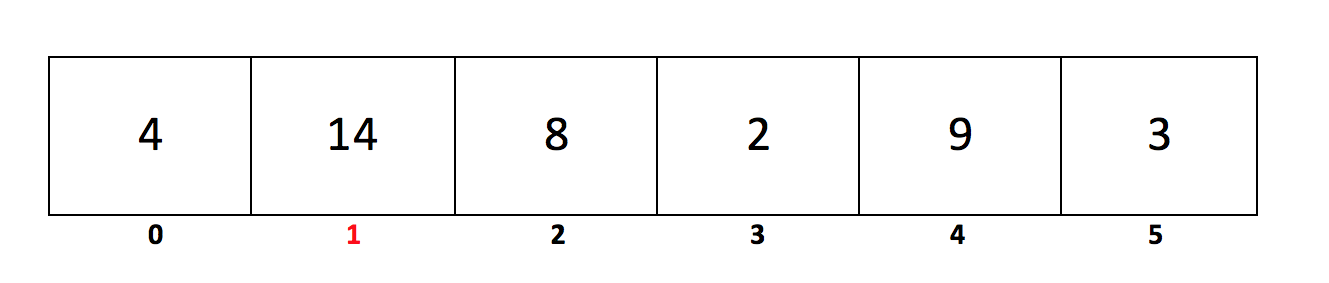
3) max

Implement the function named max to satisfy the following requirements.

When max is called with an empty array for parameter a, it should return 0.

When max is called with a non-empty array for parameter a, it should return the largest element in the array. Hint: try to call your maxIndex function from within max to avoid having another loop inside of your max function.

For example, with the array from the example for (2) above, we can see that 14 should be returned because it is the maximum element in the array.

4) mode

Implement the function named mode to satisfy the following requirements.

You can assume the array of numbers given to mode contains only integer values.

When mode is called with an empty array for parameter a, it should return 0.

When mode is called with a non-empty array for parameter a, it should return the element which occurs most frequently in the array a. For example, mode([0, 1, 1, 2, 2, 1, 3]) should return 1 because the number 1 occurs 3 times and no other number occurs that many times.

When an array contains multiple modes, return the smallest of the modes. For example, mode([0, 2, 2, 1, 1]) should return 1 because although both 1 and 2 are modes of this array, 1 is smaller than 2.

Hints! This is a conceptually challenging function to come up with and will stress your understanding of arrays and indexing. Give yourself plenty of time to work with this function.

Hint #1 - You will need to establish another array of numbers to count the number of times each value occurs in the parameter array a. How might you use the index numbers of this array to keep track of how many times a number in a has been counted?

Hint #2 - Start by trying to get mode to work only for arrays which contain the numbers 0, 1, and 2. For example: [0, 0, 1, 1, 2, 1] . You may find it useful to find the max value in such an array. For now, this will tell you how many elements your counting array will need to have. You should initialize all elements in your counting array to 0.Then, after you have counted the numbers in a, you may find it useful to find use your maxIndex function.

Hint #3 - Once you have convinced yourself you have completed Hint #2, try using arbitrary positive values such as [10, 20, 20, 30].

Hint #4 - Only after you have completed hint #3, then you should improve your mode function to work for arrays that also contain negative numbers, such as: [0, 0, -5, -5, 2, 1] which should return -5. You may find it useful to find the min of your input array and know its range between max and min.

For example, the following array has three separate occurrences of the number 4. Its mode is 4 because there are no other numbers which have more occurrences.

Let's go a little more in-depth. Say we have the following input as an array:

The intermediate array we should create to keep track of how many occurrences we have of each element should look like this:

This is because element 0 has 1 occurrence, element 1 has 3 occurrences, and element 2 has 2 occurrences. We go from thinking about 0 as an element in our input array to thinking about 0 as an index in our intermediate array.

Finally, we see that the maximum amount of occurrences (or our maximum element in our intermediate array) is 3, at index 1 of our intermediate array. Therefore, 1 is our mode.